digital partitions | science game

Last week we wondered how you can distribute a cake (or something else) between three people in such a way that all three accept the distribution as good. In the case of two people, it is very simple, and it is also a situation that often happens in real life, for example, when two children have to share a chocolate bar or a sandwich: one makes the section and chooses the other, which the first will take good care of to ensure that the two parts are even. But in the case of three people – we call them A, B and C – the question becomes very complicated. One possible solution (not unique, I invite skilled readers to look for others) is the following:

A divides the pie into three parts, B chooses two parts and the remaining part is A. If B considers the two parts he chose to be equivalent, he gives C the choice between the two parts and keeps the rest (although C you also have the option to choose part A). If B considers the two pieces he has chosen to be unequal, he cuts off a part of one of them to make them equal before offering them to C; In this case, there is a piece left over which the three can be distributed in the same way: one of them (it doesn’t have to be A again) divides it into three parts, etc. In theory, the process can be repeated infinitely (or even up to the molecular level); But in practice it is not usually necessary to skip the first step, unless the triple division of A is clearly unfair.

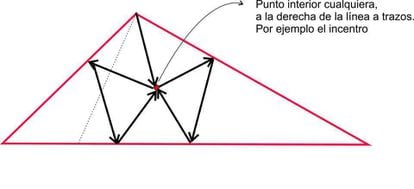
Regarding the division of an obtuse triangle into acute angles, the unnecessary condition that people often impose on themselves when trying to solve it is that all acute angles have all their vertices on the sides of the obtuse angle, and in this way it is impossible; But, as can be seen from the drawing sent by Enol Ferre, division is possible by coincidence of several vertices of acute angles at an interior point of an obtuse angle. Is this division into seven acute angles insignificant? (Note, by the way, is the “psychological” parallel with the famous nine-point problem of connecting them to four straight lines.)

natural number division

And since we talked about division and distribution, it is necessary to mention the mathematical concept of dividing a natural number, which consists in decomposing it into the sum of other natural numbers (that is, integers and positive).

Sections are one of those wonderful mathematical subjects which, from a very simple approach, and whose understanding and first developments are within the reach of anyone, opens up a field of infinite possibilities and infinite applications.

Let’s see the divisions of the first natural numbers:

The number 1 cannot be parsed into additions, so it has only one division (the number itself is considered one of its divisions).

The number 2 can be decomposed into additions in only one way: 2 = 1 + 1, therefore, it has two parts.

For 3 three divisions 3 = 2 + 1 = 1 + 1 + 1.

The 4 has five divisions: 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1.

The Five has seven divisions…

British mathematician Alfred Young (1873-1940) devised the diagrams named after him to visualize divisions:

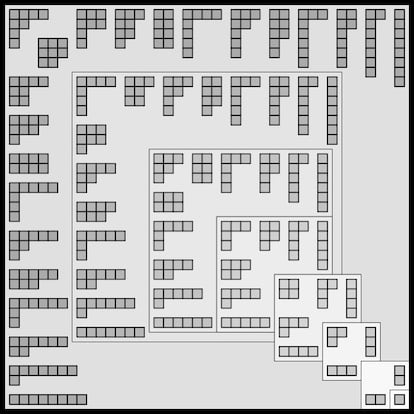
I invite experienced readers to interpret Young’s diagrams, to relate them to another topic discussed a few months ago in this section, to construct the sequence of the number of divisions of successive natural numbers, and to draw relevant conclusions.

Carlo Frappetti Writer, mathematician, and member of the New York Academy of Sciences. He has published more than 50 popular scientific works for adults, children, and youth, including “Damn physics”, “Damn maths” or “The Great Game”. He was the screenwriter of the movie “La bola de cristal”.

You can follow Thing employment Facebook social networking siteAnd Twitter NS Instagram, or sign up here to receive Our weekly newsletter