tetrahedral and serpent | science game

Beck’s formula couldn’t be simpler, as was said last week, allowing us to find a mesh polygon surface based on its interior points and perimeter:

S = I + y/2 -1

where i is the number of interior points and p is the number of perimeter points. The various ways of proving this theorem sparked a lively debate among readers, with even whether Beck’s theorem was a valid theory or just a “working formula”, argued Francisco Montesinos (see the first twenty comments of the previous installment). The question is not trivial, because between what we call ‘theorems’ and what we call ‘properties’, the difference is not qualitative but a difference of degree, since all its connotations are present in any mathematical hypothesis. Is it theorem that the sum of the angles of a triangle is 180º? Equal vertical angles? The latter can be said to be obvious (it suffices to realize that they have the same complementary angle, that is, they lack the same magnitude to reach 180 degrees); But the notion of ‘obvious’ is very subjective, and it refers us, again, to the old paradoxical cumulative inference or ‘heap’, with which we have already dealt on more than one occasion. Manuel Amoros put it in a humorous and no less eloquent manner: “If it is easy for me to understand, then this is a formula; if I find it difficult to understand, then this is a mantra: If I do not understand a damn thing, this is a theory.” (I might add: if I understand it, but I can’t prove it, it’s a guess.)

As for the temptation to extend Beck’s theory to three-dimensional space, John Reeve explained in 1957 that it is not possible, from the following corresponding example:

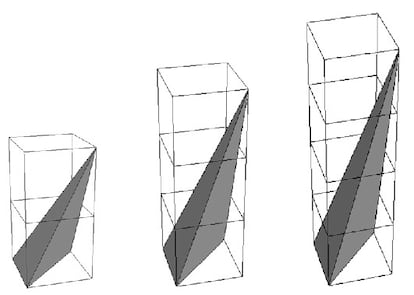
Let us consider a tetrahedron whose vertices are the points (0, 0, 0), (0, 1, 0), (1, 0, 0) and (1, 1, y) of the spatial coordinate axes, where r is a natural number (An integer and a positive). In the attached figure we see a Reeve tetrahedron, with a fixed base and a variable height, when r takes the values ​​2, 3 and 4, respectively. How does a tetrahedron prove the inapplicability of Beck’s theory in 3D space? And after this medium difficulty question, an easy question and another hard one: What is the size of a Reeve tetrahedron? Is Pick’s theorem inapplicability inference in 3D applicable to other dimensions?

As for questions related to ostomyit seems They haven’t, at the moment, caught the interest of my veteran readers (I can’t believe they’re resisting them), so they’re still hanging out.

snake game

Returning from the 3D grid to the perfect 2D grid, the 8×8 board, and taking on the topic of safe strategy games discussed in previous weeks, Ignacio Alonso suggests a problem from Peter Winkler’s highly recommended collection of math puzzles:

Adam starts his game of Snake (unrelated to Google) by checking any square on the chessboard. Eva then selects an orthogonal square next to the square marked by her partner. Thus, alternately, they each mark a square adjacent to the last one marked, forming a snake on the board. The game ends when one of them cannot check any square, thus losing the game.

Is there a box that guarantees Adam’s victory if he ticks it on the first move? In other words, is Winkler’s Snake a safe strategy game?

Carlo Frappetti Writer, mathematician, and member of the New York Academy of Sciences. He published more than 50 popular scientific works for adults, children and youth, among them “Maldita physics”, “Malditas Matematicas” or “El Gran Juego”. He was the screenwriter of The Crystal Ball.

You can follow Thing On FacebookAnd the Twitter And the Instagramor sign up here to receive Weekly newsletter.